The Matrix Code

A handy heuristic for basic linear algebra

This one gets a little mathy. Not too much. But I just had to write about a micro-breakthrough I discovered. It freed me from a very annoying routine I needed to follow to do a very simple matrix operation, and I suspect that I am not alone. It all came from a very simple graphic I created (see below).

Dive in, if you dare.

A Most Annoying Routine

No, this isn’t it.

That one’s me doing matrix multiplication. Every single time. For years.

Initially I wondered if “spreadsheet confusion” was the cause. You know that thing where they get the whole [row, column] thing completely backwards?

Nope. That’s a separate problem that’s just annoying - and solvable by a simple mental transpose: {spreadsheet}ᵀ. Cell variables, too. Hey, it works for me.

But I digress.

So, you ask… how did I actually do matrix multiplication all these years?

By writing out the two matrices on paper, dancing the pencil through a repetitive “this row, that column” routine, drawing lines, and concentrating like I was back in second grade doing times tables. Talk about feeling dumb. I told observers I was just being diligent. I envied those who could do this multiplication in their heads. Maybe they just used calculators.

Didn’t Einstein Summation Notation Help?

For those not in the know, Einstein summation notation is a shorthand where repeated variables, like the ‘j’ below, are bound, and therefore don’t vary across the implied addition that makes the shorthand notation a powerful thing. It was an immense timesaver for Einstein and others, not to mention a lifesaver for countless trees.

\(x_{ij} y_{jk}\)

No timesaver for me, though. Pencil still went bouncy-bouncy. In fact, I felt dumber.

The Breakthrough

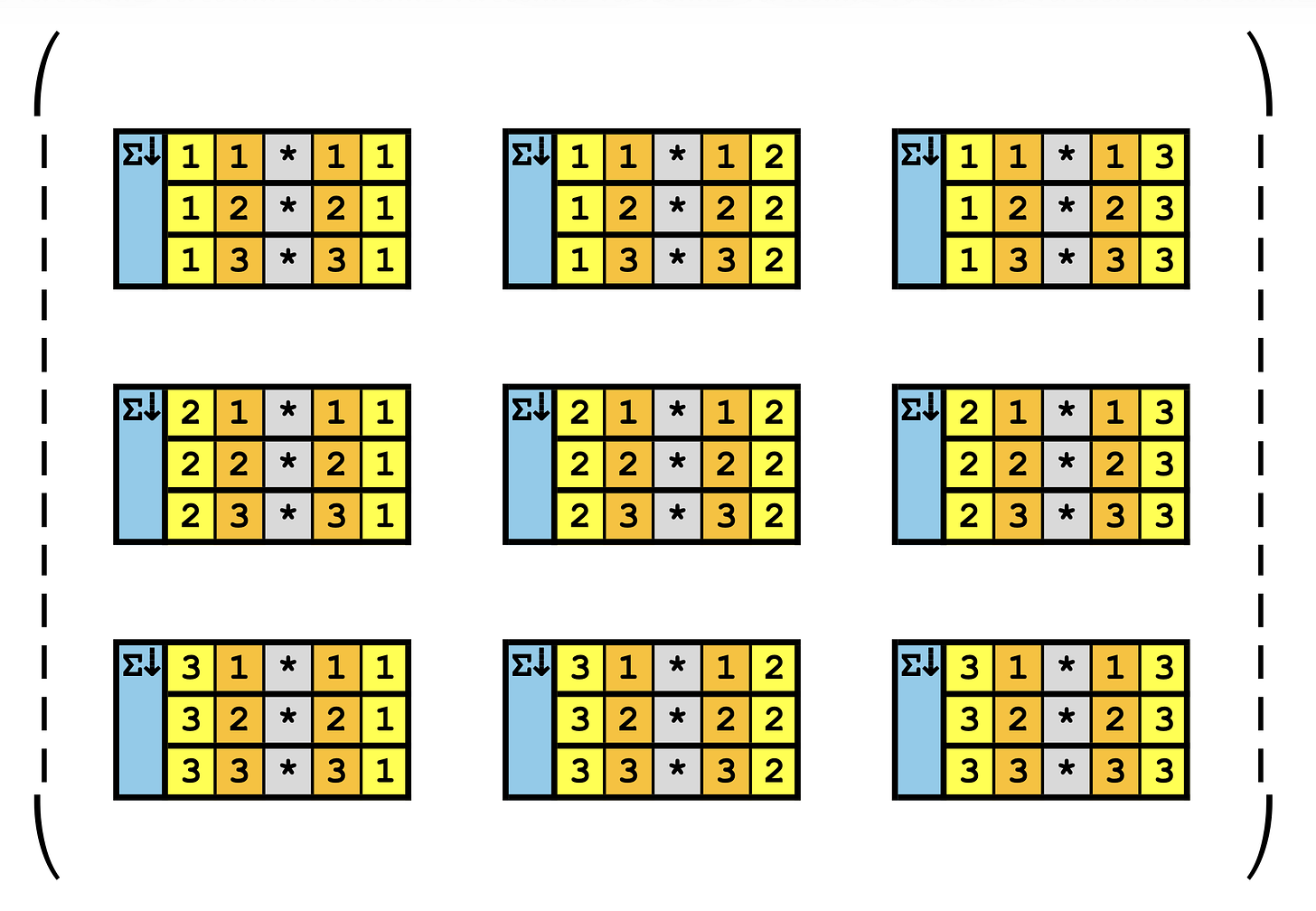
The other day, instead of the normal drill, I created this orderly chart. I hope you can see it on your phone if you are viewing it that way. It’s a representation of the output for a 3x3 matrix multiplication operation - and in color, too!

If you’re not familiar with matrix multiplication, this might be a little confusing. I’ll explain it in a minute.

For example, to get the product element for row 2, column 3, you would perform this operation:

\(z_{23} = x_{21}y_{13} + x_{22}y_{23} + x_{23}y_{33} = x_{ij} y_{jk}\)

Check this with the grid in row 2, column 3 in the picture above to get a lock on the idea.

I immediately noticed the following:

• the yellow columns signify the (row, column) of the product element

• the orange columns illustrate a repetitive pattern (1,2,3…1,2,3) across all product elements

• the blue column down the side is just the summation operation

Wait a minute! The orange column patterns don’t change. Why is that?

Claude helped bring it home:

You've visually encoded the most fundamental distinction in all of tensor mathematics: free vs bound indices.

• Yellow = Free indices

• Orange = Bound indices

Einstein summation made visual.

Orange columns don’t change because j is bound. Okay, duh.

\(x_{i\textcolor{orange}{j}} y_{\textcolor{orange}{j}k} = z_{ik}\)

That chart is now hanging up on my wall. No more dancing pencil. And I now “see” all bound variables as orange. Nice!

I hope this helps you if you’ve had a similar block.

Enjoy!